Computer Science 245: Data Structures and Algorithms



David Galles
Computer Science
Univerisity of San Francisco

Programming Assignment 4: Search

Dijkstra's algorithm allows us to find the shortest path from one vertex in a graph to all other vertices in the graph. It is a great algorithm for finding the shortest path in an explict graph (that is, a graph that is defined using an adjacency list or an adjacency matrix). However, if the graph is implicit (we don't have the actual graph, just rules for how it can be created), then Dijkstra's algorithm can be problematic. Especailly if the entire explict graph is too big to store in memory.

Implicit Grpah vs Explicit Graph

An Explcit grpah is one where you have, in memory, a list of all vertices and all edges in the graph. All of the graphs we have seen so far in this class have been explict. An implict graph is one where we have rules for creating vertices and edges, but do not have the entire graph in memory. Let's take a look a t a simple implicit graph: the search graph for the sliding tile puzzle.

Sliding Tile Puzzle

The sliding tile puzzle is a simple toy that consists of a number of tiles, and an empty space that can be used to move tiles around. (wkikpedia link), Interactive version. The sliding tile puzze defines a graph, where each state of the puzzle is a vertex, and there are edges between states if they can be reacted by a single move:

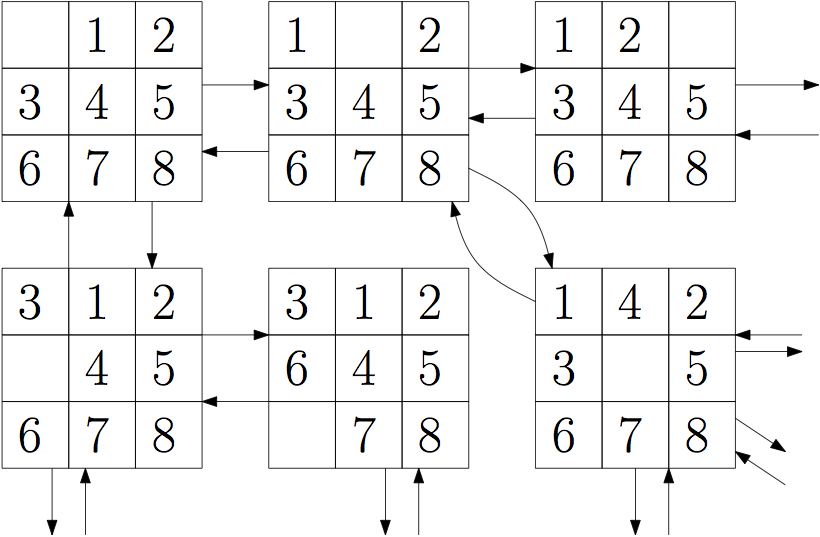
We can define the search problem by giving:

Dijkstra in an implicit graoh

Recall how Dijkstra's algoritm worked, in broad strokes:

In class we discussed how to use a priority queue to pick the cheapest unknown vertex, and we further discuesses two ways of implementeing that priority queue when distances were updated: Actually going into the queue to rearrange elements, and adding duplicate entries to the queue. We will use the second of these (adding duplicate entires to the priority queue) and, generalize Dijstra's algorithm for implicit graphs as follows:

General Search Algorithm for Implicit Graphs

We will maintain 2 lists, an "open list" and a "closed list" The "closed list" will be a list of all states (vertices in our implicit graph) that are Known. The Open lists is a list of all states that we can get to from the iniitial state, but whose shortest path is not necessarily known yet.

Uniform Cost Search

If the "best vertex" is the vertex that is the closest vertex to the initial state, then what we have is "Uniform Cost Search", which is essentially Dijkstra's algorithm on an implicit graph. We are guaranteed to find the shortest path to the goal, but we are expanding (that is removing from the open list and adding to the closed list) a potentially large number of vertices. If the branching factor (that is, number of children per state) is b, and the length of the path to the goal is d, then we are expanding bd states, which can be a large number of states. We can do a little better by adding some more information

Heuristics

Instead of just expanding the state that is closest to the intial state, it would be better to also take advantange of how close a state is to the goal Of course, we do not know how close any state is to the goal state (that is what we are trying to find out by searching!) but we can make a guess as to how far a state is from the goal state. A heuristic is just a guess of how close a particular state is to the goal state. Which heuristic to use depends on the specific problem you are trying to solve. Let's look at the heuristic for the Sliding Tile puzzle:

Sliding Tile Heuristic -- Manhattan Distance

An easy to calculate heuristic for the sliding tile puzzle is Manhattan Distance - The distance each tile needs to move from its current position to its final position in the solution, assuming tiles can only move horizontally or vertically (like going between intersections in Manhattan, where you can only take east/west streets or north/south strees). For example for the following initial and goal positions:

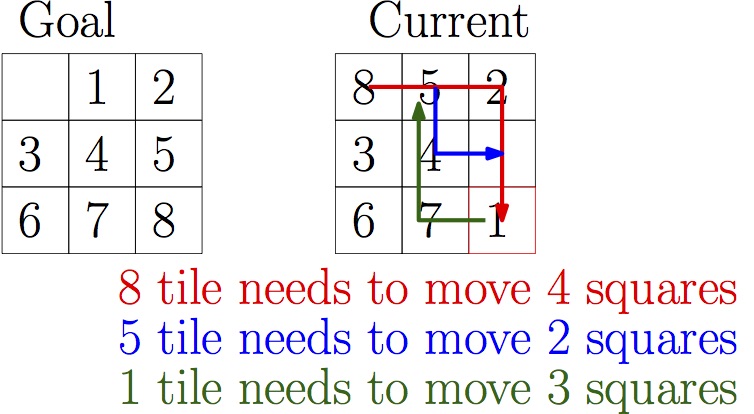
The Current state has a manhattan distannce of 9 to the goal state in the above example

A*

This leads us to a new variant of the generic searching algorithm. The only difference is what makes a state the "best" state to consider next. When is a state the "best" to expand? When that state is on the optimal path from the initial node to the goal. How can we determine that? Unfortuneatly, we can't know for sure, but we can make a pretty good guess. If we have a heuristic function that gives a guess of the cost to get from a state to the the goal, then for each state s, we know:

So, the estimated cost to get from the inital state to the goal through s is just the cost to get from the initial state to s, plus the estimate of the cost to get from s to the goal

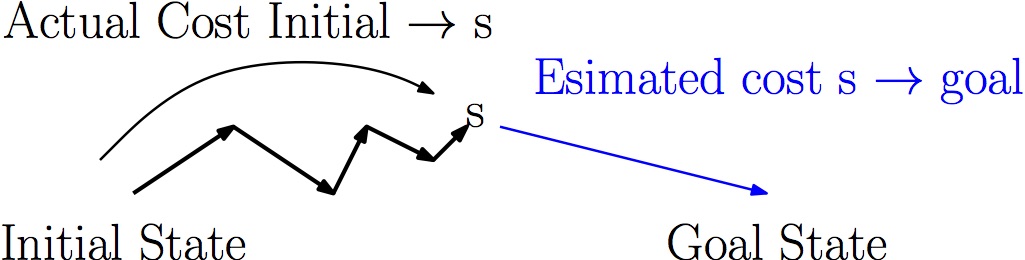
A* is a search algorithm that always expands the next state that has the best estimated cost to the goal.

So, if:

Then A* is just a general search algorithm where the "best" state s is the state with the minimum g(s) + h(s) value. That is, the state whose actual cost from the initial state, plus the estimated cost from s to the goal, is minimized

A* and Uniform Cost search both find optimal paths to the goal. However, A* will (in general) expand fewer states -- so will take less time (and less memory) than Uniform Cost Search. If, howeveer, you are willing to give up on optimallity, you can have an even more efficient algorithm

Greedy Search

Greedy search picks as the "best" state the one that is closest to the goal. The idea behind greedy search is not to find the cheapest possible solution, but to find a solution as quickliy as possible. Greedy seach always picks the node with the smallest heuristic (h) value. For problems with a very large search space, greedy can often find a solution when Uniform Cost Search or A* would take way too long or require way too much memory. For example, solving hard 15 puzzles (or 24-puzzles, or the like) can take prohibitively long using A*, but can be solved relatively quickly using Greedy (at the cost of geting a non-optimal solution)

Search Overview

Where f(s) is determined by the kind of search you are doing:

Implemenation Details

To do a search over an implicit graph, you need to:

Open List

We will use a min-heap based priority queue to implement the open list. We will insert priority / value pairs, where the value is a state, and the priority is a float. You will need to write this priority code yourself, and not rely on Java library code

Closed List

We will used a Hash Table to implement the closed list. The states will have a method hashCode and equals that the hash table will use to insert into the table and check for membership. You can use either open or closed hashing. You are not allowed to use a build-in Java collection for this, but need to write the hash table on your own. Your hash table should use the hashCode method of the states that are inserted to create the appropriate hash value.

States

States will need to implement the following interface: State.java 


public interface State {

	/**
	 * Return an array of all of the children of this state.  The returned array 
	 * should be just large enough to hold all of the children of this state.
	 * @return Array of children of this state
	 */
	public State[] getChildren();
	
	/**
	 * Return the parent of this state (that is, the state that generated this
	 * state), or null if this is an initial state
	 * @return
	 */
	public State getParent();
	
	/**
	 * Returns true if this state is equal to another state, ignoring parents
	 * @param other The state to compare to 
	 * @return True if the states are equal
	 */
	
	public boolean equals(State other);
	
	/**
	 * String representation of the state
	 * @return
	 */
	public String toString();

	/**
	 * Return the distance of this state from the initial state.  
	 * @return
	 */
	public float gValue();
	
	/**
	 * Hash code for this state.  States that are equal (via the above equals) need
	 * to have the same HashCode
	 * @return
	 */
	public int hashCode();
	
	/**
	 * Returns a string representation of the solution path.  See concrete states for more information
	 * @return String representation of the standard solution path
	 */
	public String solutionPath();
	
	/**
	 * Returns a more verbose representation of the solution path.  See concrete states for more information.
	 * @return String representation of the verbose solution path
	 */
	public String solutionPathExtended();
	
	
	/**
	 * Returns the (estimated) distance from this state to an arbitrary different state.  
	 * The heuristic (h) value is the estimated distance of that state from the goal.
	 * @return Estimated distance to the state
	 */
	public float distanceToState(State otherState);
}

A few things to note about this state interface

Sliding Tile State

The sliding tile state should have 2 constructors, the "external" constructor used to create the initial (and goal) states, and an "internal" constructor, used by getChildren to create the child states. The external constructor needs to be of the from 

public SlidingTileState(int width, int height, int tiles[])

Where tiles is a one-dimensional array of tiles, listing the tiles in row major order. '0' will be used for the empty tile. So, to create the tile:

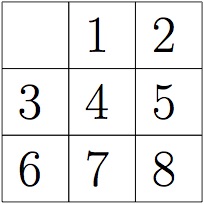
we would use the constuctor call 

new SlidingTileState(3,3,  new int[] {0,1,2,3,4,5,6,7,8})

And to create the tile

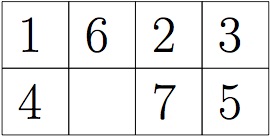
we would use the constuctor call 

new SlidingTileState(4,2,  new int[] {1,6,2,3,4,0,7,5})

The internal constructor will need to have (at least!) an extra parameter for the parent, and may have other different parameters as well (you may, for instance, want to pass in the tiles as a 2D array, or something else convienient based on your internal representation.)

gValue

For the sliding tile puzzle, the gValue of a particular state s is the number of moves from the initial state to state s. I recommend that you cache this value in the state, but you can reconstruct it on every call to gValue if you prefer.

toString

toString should return a string representation of the board, in a nice visual format, like: 

+-+-+-+
| |1|2|
+-+-+-+
|3|4|5|
+-+-+-+
|6|7|8|
+-+-+-+

or, for a 4x2 puzzle 

+-+-+-+-+
|2|3|7|6|
+-+-+-+-+
| |1|4|5|
+-+-+-+-+

or, for a 4x4 puzzle 

+--+--+--+--+
| 1| 5| 2| 3|
+--+--+--+--+
| 4| 6|10| 7|
+--+--+--+--+
|12| 9|  |11|
+--+--+--+--+
|13| 8|14|15|
+--+--+--+--+

solutionPath

solutionPath should return a string that consists of a list of the tiles to move to get from the initial state to the final state, separated by commas. For example, for the following initial and final states: 

Initial:
+-+-+-+
|1|4|2|
+-+-+-+
|3|5|8|
+-+-+-+
|6|7| |
+-+-+-+

Final:
+-+-+-+
| |1|2|
+-+-+-+
|3|4|5|
+-+-+-+
|6|7|8|
+-+-+-+

The solutionPath should return: 

8,5,4,1

Since you can get to the final state by first moving the 8 tile, then the 5 tile, then the 4 tile, then the 1 tile

solutionPathExtended

solutionPathExtended should return a string representing a concatenation of each state along the path from the initial to the final state. So, for the above problem, solutionPathExtended should return 

+-+-+-+
|1|4|2|
+-+-+-+
|3|5|8|
+-+-+-+
|6|7| |
+-+-+-+
-------
+-+-+-+
|1|4|2|
+-+-+-+
|3|5| |
+-+-+-+
|6|7|8|
+-+-+-+
-------
+-+-+-+
|1|4|2|
+-+-+-+
|3| |5|
+-+-+-+
|6|7|8|
+-+-+-+
-------
+-+-+-+
|1| |2|
+-+-+-+
|3|4|5|
+-+-+-+
|6|7|8|
+-+-+-+
-------
+-+-+-+
| |1|2|
+-+-+-+
|3|4|5|
+-+-+-+
|6|7|8|
+-+-+-+

distanceToState(State otherState)

distanceToState should return the Manhattan Distance between the two states. That is, for each tile in the puzzle, count the number of spaces it would need to move to get into the required position. Remember that the 0 is an empty space (and not a tile!) and should not be considered as part of the Manhattan Distance.

getChildren

getChildren should return an array of all of the children of the state. Note that there will be a different number of children, depending upon the position of the blank space: between 2 (if the blank space is in a corner) to 3 (for an edge) to 4 (for the middle). You should return an array that is just large enough to hold all of the children

Maze Position State

The required constructor for the MazePositionState is as follows: 

public MazePositionState(String maze, int x, int y)

Where maze is a string representing the maze, with a space characeter ' ' for traversable spaces, and a non-space character for non-traversable spaces. The string will use the end-of-line character '\n' to separate rows of the maze. x and y represent the (x,y) position, starting at (0,0) for the upper-left corner of the maze

As with the slidingTileState, you will also likely want a separate constructor that you use when you generate children. I strongly recommend that there be one 2D array that all states use (that is, each state will have a pointer to the same overall maze, in addition to a local x,y position)

getChildren

getChildren returns a state for each posistion that is reachable in a single step. A position is reachable if it is adjacent to the current position (diagonals allowed) and is not blocked. For the 4 positions that are immediatley above, below, left, and right of the current postion, they are not blocked if the space is traversable. For the diagonals, the spaces surronding the new position must also be traversrable.

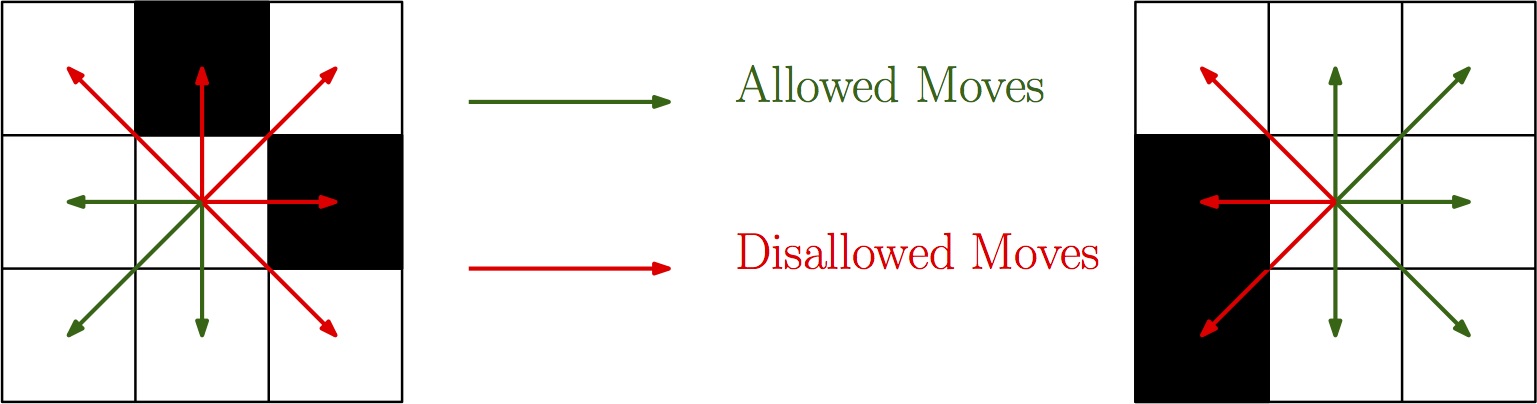
From the postion (x,y), you can move to position (x,y+1), (x,y-1), (x+1,y), and (x-1,y), assuming the desitnation position is traversable. In addition, you can move along the diagonal to position (x+1, y+1) if positions (x+1,y+1) and positions (x,y+1) and positions (x+1,y) are traversable, and likewise for the other 3 diagonals

gValue

The gValue of a state s is the sum of the legths of the subpaths from the initial state to s. Non-diagonal subpaths have a length of 1, while diagonal subpaths have a length of √ 2  (you could just ise 1.4142f if you like, but this is likely a good place for a constant!). As with the sliding tile puzzle, I would recommend caching this value, but you can recalculate it every time if you prefer.

toString

toString for a state should just return the (x,y) position of the state, such as (3,4)

solutionPath

solutionPath should return a string of x,y positions to get from the initial state to the final state, separated by commas. Something like:

(1,1),(1,2),(1,3),(1,4),(2,5),(3,6),(4,6),(5,6),(6,6),(7,6),(8,7),(9,7),(10,8),(10,9),(10,10),(10,11),(10,12),(10,13),(10,14),(9,14),(9,15),(9,16),(9,17),(10,17),(11,17),(12,17),(13,17),(14,17),(15,17),(16,17),(17,17),(18,17)

solutionPathExtended

solutionPathExtended should return a string representing the entire map, with a . character at each position along the path. Something like: 

********************
*.    **     *     *
*.        ** *  *  *
*.***     ** *  *  *
*. ***    **    *  *
* .  ************  *
*  .....           *
*       ..    ******
*   ***   .        *
*    *****.        *
********  . **     *
*         .     ****
*    *****.   ******
*     ****.        *
*        ..        *
*  **  * .*        *
*  **    .**********
*        ..........*
********************

The Assignment

For this project, you will need to create the following classes

Extra Credit

For up to 50 project points, you can add a 3rd problem domain: sliding tile puzzles with differing piece sizes. This new type of sliding tile puzzle has rectangular tiles that can have different sizes. Wikipedia has a nice explanation of these puzzles, and there are some nice interactive examples on the web

Your implementation will need to follow the same interface as the standard sliding tile puzzle. You will write a class SlidingTileState2 that implements the State interface. The constructor for SlidingTileState2 should take 3 parameters:

So, the board:

Would be created with the contstructor

 new SlidingTileState2(4,5,"2 2 0 0,2 1 2 0,2 1 2 1,1 1 0 2,1 1 1 2,1 2 0 3,1 2 1 3,2 1 2 3,2 1 2 4");

Your toString should produce a pretty version of the puzzle, for the above puzzle, something like:

+------------+
|+----++----+|
||****||****||
||****|+----+|
||****|+----+|
||****||****||
|+----++----+|
|+-++-+      |
||*||*|      |
|+-++-+      |
|+-++-++----+|
||*||*||****||
||*||*|+----+|
||*||*|+----+|
||*||*||****||
|+-++-++----+|
+------------+

would be nice, but you can use your own creativity here

solutionPath should return a list of substrings of the form ((x1,y1),(x2,y2)) separated by commas, where (x1,y1) is the upper-left corner of the piece to move, and (x2,y2) is the upper-left corner of the location to move the piece to (where (0,0) is the upper-left position of the entire board). So, for the inital and final states: 

Initial:
+------+
|+-++-+|
||*||*||
|+-++-+|
|+-+   |
||*|   |
|+-+   |
+------+
Final:
+------+
|   +-+|
|   |*||
|   +-+|
|+-++-+|
||*||*||
|+-++-+|
+------+

A valid solution path would be: 

((0,1),(1,1)),((0,0),(0,1))

For the extended solution path, concatenate a series of boards, just like the original sliding tile puzzle. For the above example, and extended solution path would be 

+------+
|+-++-+|
||*||*||
|+-++-+|
|+-+   |
||*|   |
|+-+   |
+------+
--------
+------+
|+-++-+|
||*||*||
|+-++-+|
|   +-+|
|   |*||
|   +-+|
+------+
--------
+------+
|   +-+|
|   |*||
|   +-+|
|+-++-+|
||*||*||
|+-++-+|
+------+

Extra Credit Hints

Extra Credit Provided Files

Provided Files

Univeristy of San Francisco Department of Computer Science