Graphs

Due date: Apr 16, 2007

Your goal in this project is to build some computer science course dependency graphs and then run some simple (backtracking) algorithms. For example, your software will need to answer such questions as:

• Which courses are needed before you can take 490
• How fast in terms of number of semesters can you finish 490?
• How many courses depend directly or indirectly on 112?
• List all courses you can take after you finish 210
• List all courses without prerequisities; I.e., list courses that have no incident (incoming) edges?

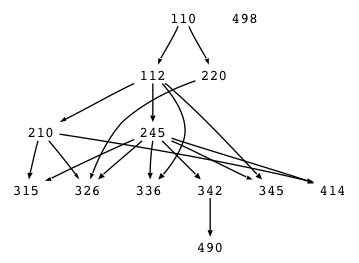
Your program will accept as input a graph such as the following partial USF course dependency graph:

The input to your program will actually be an edge list (followed by a sequence of commands). Each edge is on a separate line that maps one node to another:

110 -> 112
112 -> 210
110 -> 220
112 -> 245
210 -> 315
245 -> 315
210 -> 326
220 -> 326
245 -> 326
112 -> 336
245 -> 336
245 -> 342
112 -> 345
245 -> 345
210 -> 414
245 -> 414
342 -> 490
498

Graph operations

After the graph edge list, you can type in a series of commands:

• print
  Prints list of pages in nodes out in the order they were specified.
• len start stop
  Prints the minimum number of edges traversed to go from start to stop. If stop == start, print 0.
• nodes start stop
  Prints all nodes along all paths from start to stop. The list of nodes must be sorted.
• reach start
  Prints the list of all nodes reachable from start.
• roots
  Print the graph roots. A graph root is any node has no incident (incoming) edges.

Here are some sample commands:

print
len 112 112
len 110 112
len 110 345
nodes 110 490
len 110 490
nodes 110 345
len 110 345
reach 110
reach 326
roots

and the associated output:

...edge list in order specified...
len 112 -> 112 = 0
len 110 -> 112 = 1
len 110 -> 345 = 2
nodes 110 -> 490 = [110, 112, 245, 342, 490]
len 110 -> 490 = 4
nodes 110 -> 345 = [110, 112, 245, 345]
len 110 -> 345 = 2
reach 110 = [110, 112, 210, 220, 245, 315, 326, 336, 342, 345, 414, 490]
reach 326 = [326]
roots = [110, 498]

Implementation

You will implement a Graph class, which is a group of Nodes. A Graph is just a mapping from node name to Node object and defines the methods implementing the required algorithms. A Node has a name and a list of edges. Note that the list of edges must be List<String> rather than List<Node> because you can reference a node in the edge list before you have defined it. By using string node names in the edge list, you can always look up the nodes in the Graph mapping.

You must not use Graph fields as temporary variables for the various algorithms. To avoid these, you will typically define to methods for each algorithm as we did in other recursive algorithms. For example, getAllNodes() would look like this:

/** Return a sorted list of all nodes between start and stop, inclusively */
public List<Node> getAllNodes(String start, String stop) {
    Set<Node> pathNodes = new HashSet<Node>();
    _getAllNodes(nodes.get(start), nodes.get(stop), pathNodes);
    List<Node> nodeList = new ArrayList<Node>(pathNodes);
    Collections.sort(nodeList);
    return nodeList;
}

protected boolean _getAllNodes(Node p, Node stop, Set<Node> pathNodes) {
    ...
}

Here is a Graph outline:

/** A set of nodes */
public class Graph {
    /** Map a node name to the node */
    ... define nodes field here ...

    public Node addNode(String name) {
    }

    public void addEdge(String name, String target) {
    }

    /** Return sorted list of all nodes between start and stop, inclusively */
    public List<Node> getAllNodes(String start, String stop) {
        Set<Node> pathNodes = new HashSet<Node>();
        _getAllNodes(nodes.get(start), nodes.get(stop), pathNodes);
        List<Node> nodeList = new ArrayList<Node>(pathNodes);
        Collections.sort(nodeList);
        return nodeList;
    }

    protected boolean _getAllNodes(Node p, Node stop, Set<Node> pathNodes) {
    }

    public int getMinPathLength(String start, String stop) {
    }

    /** Return a sorted list of all nodes reachable from start, inclusively */
    public List<Node> getAllReachableNodes(String start) {
    }

    public List<String> getRootNames() {
    }

    /** Print out an edge list for graph */
    public String toString() {
    }
}

Here is Node:

/** A node with a name and list of directed edges (edges do not
 *  have labels).
 */
public class Node implements Comparable {
    ... define name field ...

    /** The list of node names targeted by edges.  Use symbolic names
     *  rather than Node ptrs so we can do forward refs easily.
     */
    ... define edges field ...

    public Node(String name) {
    }

    /** Add an edge if it doesn't already exist */
    public void addEdge(String target) {
    }

    public String toString() {
        return name;
    }

    /** This method allows us to test a Node against a list for
     *  membership and is also needed for the Collections.sort().
     */
    public int compareTo(Object o) {
        return name.compareTo(((Node)o).name);
    }
}

As you can see in the above code, you should use Java generics (analogous to C++ templates) in your code.

We will go over each algorithm in class.

Unit testing

You will need to test your software in some way, and I've build the parser in such a way that you can get the output easily as a string. For example, here are two unit tests that I provide for you:

public void testPrint() throws IOException {
    Tool t = new Tool();
    String g =
        "110 -> 112\n" +
        "112 -> 326\n" +
        "print\n";
    StringBufferInputStream in = new StringBufferInputStream(g);
    String found = t.exec(in);
    String expecting =
        "Graph:\n" +
        "110 -> 112\n" +
        "112 -> 326\n";
    assertEquals(expecting, found);
}

public void testLen() throws IOException {
    Tool t = new Tool();
    String g =
        "110 -> 112\n" +
        "112 -> 326\n" +
        "len 110 326\n";
    StringBufferInputStream in = new StringBufferInputStream(g);
    String found = t.exec(in);
    String expecting =
        "len 110 -> 326 = 2";
    assertEquals(expecting, found);
}

I strongly suggest that you created number of unit tests to ensure that your software works properly.

Visualizing graphs

If you would like to visualize your test graphs, you can use graphviz's DOT format. There is a particularly nice Mac OS X version of Graphviz. Just wrap your edge list in the following text:

digraph mygraph {
  node [shape=plaintext, fixedsize=true, fontsize=11, fontname="Courier",
        width=.4, height=.2];
  ranksep=.4
  edge [arrowsize=.5]
  ordering=out

...your edges/nodes...

}

Resources

Don't panic. I provide you with a complete parser that handles loading the graph and executing commands. These commands, in turn, invoke methods on your Graph object that you must implement.

• Token.java
• Parser.java
• Lexer.java
• Graph.java
• Node.java
• Tool.java
• TestGraph.java

Project deliverables

Submission

You will submit a jar file called graph.jar containing source and *.class files into the submit directory:

/home/submit/cs245/userid

(Use Java 1.5 or lower to compile your classes). For example, I would submit my project as file:

/home/submit/cs245/parrt/graph.jar

Grading

We will run your program via

java -cp ".:/home/submit/cs245/userid/graph.jar" Tool < test-input-file

We will assign points as follows:

There are 2 style points points for each method. If I don't like the style of coding, I can deduct up to two points per method. For each method that causes an exception, I will deduct at most 1 point. Naturally, if the method doesn't work, you get zero for that method.

10 points off if your jar is messed up or your classes or have wrong case etc... I.e., anything that prevents us from being able to run your library "out of the box".

Reminder: There is no such thing as a late project; late projects get a zero score. Projects are due the instant class starts at 9:40 a.m. and your jars must be in the submit directory.