Sample Questions
- The following array is to be sorted using radix sort
(base-10). Show the result after sorting each digit:
218 326 654 182 335 318 125 322 911 251 807 302 224 731 435 152 After the first pass
911 251 731 182 322 302 152 654 224 335 125 435 326 807 218 318 After the second pass
302 807 911 218 318 322 224 125 326 731 335 435 251 152 654 182 After the third pass
125 152 182 218 224 251 302 318 322 326 335 435 654 731 807 911
- You are about to partition the following list, using the last element as a pivot:
10 41 4 16 17 8 30 2 11 29 22 20
Show the list after the partition step.
10 11 4 16 17 8 2 20 41 29 22 30
- The following elements are inserted into a hash table of
size 11 (with a hash function h(x) = x % 11) (in this order): 25, 3, 14, 4, 36
- 25 % 11 = 3, 25 % 5 + 1 = 1
- 3 % 11 = 3, 3 % 5 + 1 = 4
- 14 % 11 = 3, 14 % 5 + 1 = 5
- 4 % 11 = 4, 4 % 5 + 1 - 5
- 36 % 11 = 3, 36 % 5 + 1 = 2
- Show the resulting hash table, assuming open hashing (separate chaining, closed addressing)
- Show the resulting hash table, assuming closed hashing (open addressing) and linear probling
- Show the resulting hash table, assuming closed hashing (open addressing) and quadratic probling
- Show the resulting hash table, aassiming closed hashing (open
addressing) and double hashing (second hash function: hash2(x) = (x %
5) + 1)
25 4 36 3 14 0 1 2 3 4 5 6 7 8 9 10
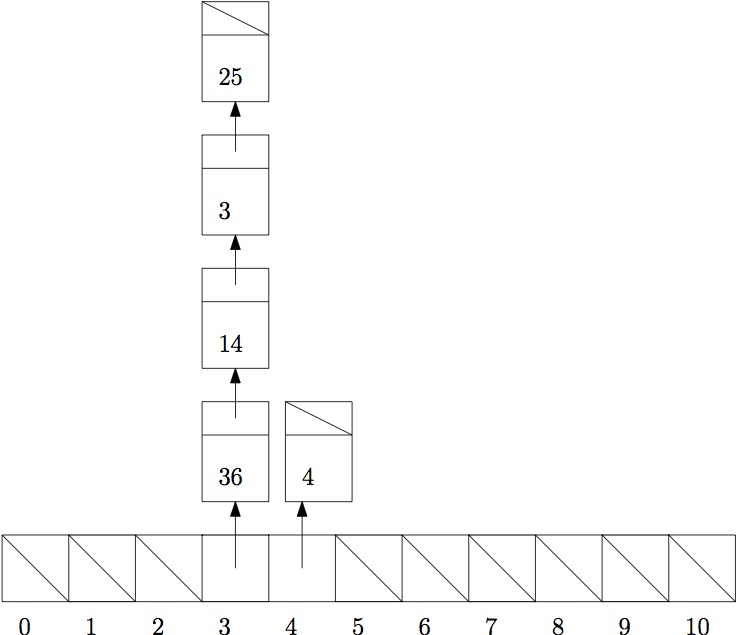
25 3 14 4 36 0 1 2 3 4 5 6 7 8 9 10 36 25 3 4 14 0 1 2 3 4 5 6 7 8 9 10 - Given the following Data Strutures
class Edge { public int neighbor; public Edge next; } class AdjListGraph { pubic int numVertex; public Edge[] edges; } class AdjMatrixGraph { public int numVertex; public boolean[][] adjMatrix; }Write a function that takes as input an adjacency list representation of a graph, and returns the adjacancy matrix representaion of the same graph.AdjMatrixGraph adjMatrixFromAdjList(AdjListGraph G) { AdjMatrixGraph returnGraph = new AdjMatrixGraph(); returnGraph.adjMatrix = new boolean[G.numVertex][G.numVertex]; returnGraph.numVertex = G.numVertex; for (int i = 0; i < G.numVertex; ++) { for (Edge tmp = G.edges[i]; tmp != null; tmp = tmp.next) { returnGraph[i][tmp.neighbor] = true; } } return returnGraph; } -
Consider the following (very silly) function that takes a graph as input:
class Edge { public int neighbor; public int cost; public Edge next; } class Graph { public int numVertex; public Edge edges } int Strange(Graph G) { int total = 0; for (v = 0; v < G.numVertex;v++) { for (Edge tmp = G.edges[v]; tmp != null; tmp = tmp.next) { for (int i = 0; i < G.numVertex; i++) { if (i == tmp.neighbor) total += tmp.cost; } } } return total; }-
(5 points) What does this function compute?
The sume of the costs of all the edges in the graph
-
(5 points) What is the running time of this function, as a function of the number of vertices V and edges E in the graph?
For each eadge in the graph, we are going through a loop of all V vertices. Since we are spending V time for each of the E edges, the total time is O(VE)
-
(5 points) What does this function compute?