Computer Science 245
Spring 2015
Bonus Project:  Spanning Trees
Due Wednesday, May 13th, 2015

For your bonus final project, you can implement Kruskal's algorithm for finding a minimal cost spanning tree. This project will combine Graphs, Kruskal's algorithm, Disjoint sets, Hash Tables and Lists (whew!). Successfull completion of this project can add up to 50 points to your projects grade.

 Nodes with Labels

For this assignment, each vertex in the graph will be labeled with an arbitrary string. How can we run Kruskal's algorithm when the vertices are not integers? First, we will assign an integer to each vertex string (the easiest way to do this is to assign the first string we see to 0, the second string we see to 1, etc). We can then store the vertex strings in an array, where the index of the array is the number that we assign to the vertex string stored at that index. For instance, if the data contains the vertex names “HRN 240”, “LM 206” and “GLE 14”, we can assign 0 to “HRN 240” (storing the string “HRN 240” at index 0 of our array), assign 1 to “LM 206” (storing the string “LM 206” at the index 1 of our array) and we can assign 2 to “GLE 15” (storing the string “GLE 14” at index 2 of our array). Now, given any number n, it is easy to find the appropriate string assigned to that number (by looking at index n in our array).

How can we get an index given a string? One method would be to search through our entire array looking for the appropriate string. A better solution (and the solution that you are required to use for this assignment) is to create a hash table to store the vertex string / vertex number combinations. You can use the vertex string as the key to enter the vertex number into the hash table (so each hash table entry will have a vertex number data value, and a string key value). You can use any hashig strategy that you wish, though you might find that open hashing is slightly easier to implement. Note that you are not allowed to use any built-in hash table functionality in Java, you will need to write the hash table yourself!

Implementing the Graph

One you have created your array of vertex names and your hash table to look up vertex numbers, you are ready to build the graph. Your graph need not contain any information about which vertex number is assigned to which node string – that information can be kept entirely in you node string array and your hash table. You will find the hash table quite useful when creating the graph, however!

Kruskal's Algorithm

Once you have your graph, your are ready to run Kruskal's Algorithm. Enter all of the edges into a list, and then sort it based on the edge cost. Then repeatedly remove the smallest edge, check to see if it will cause a cycle (using your disjoint set data structure), and add it to the spanning tree if it does not cause a cycle (also updating the disjoint set)

Disjoint Sets

Your implementation of Kruskal's algorithm will use disjoint sets. Your implementation of Disjoint Sets should use union-by-rank and path compression for maximum efficiency. See the Disjoint Set notes for more details.

Quick Overview of Data Structures

So, while Kruskal's algorithm is running, you will have the following data structures:
Thus, just before you start running Prim's algorithm, your data structures might look something like:
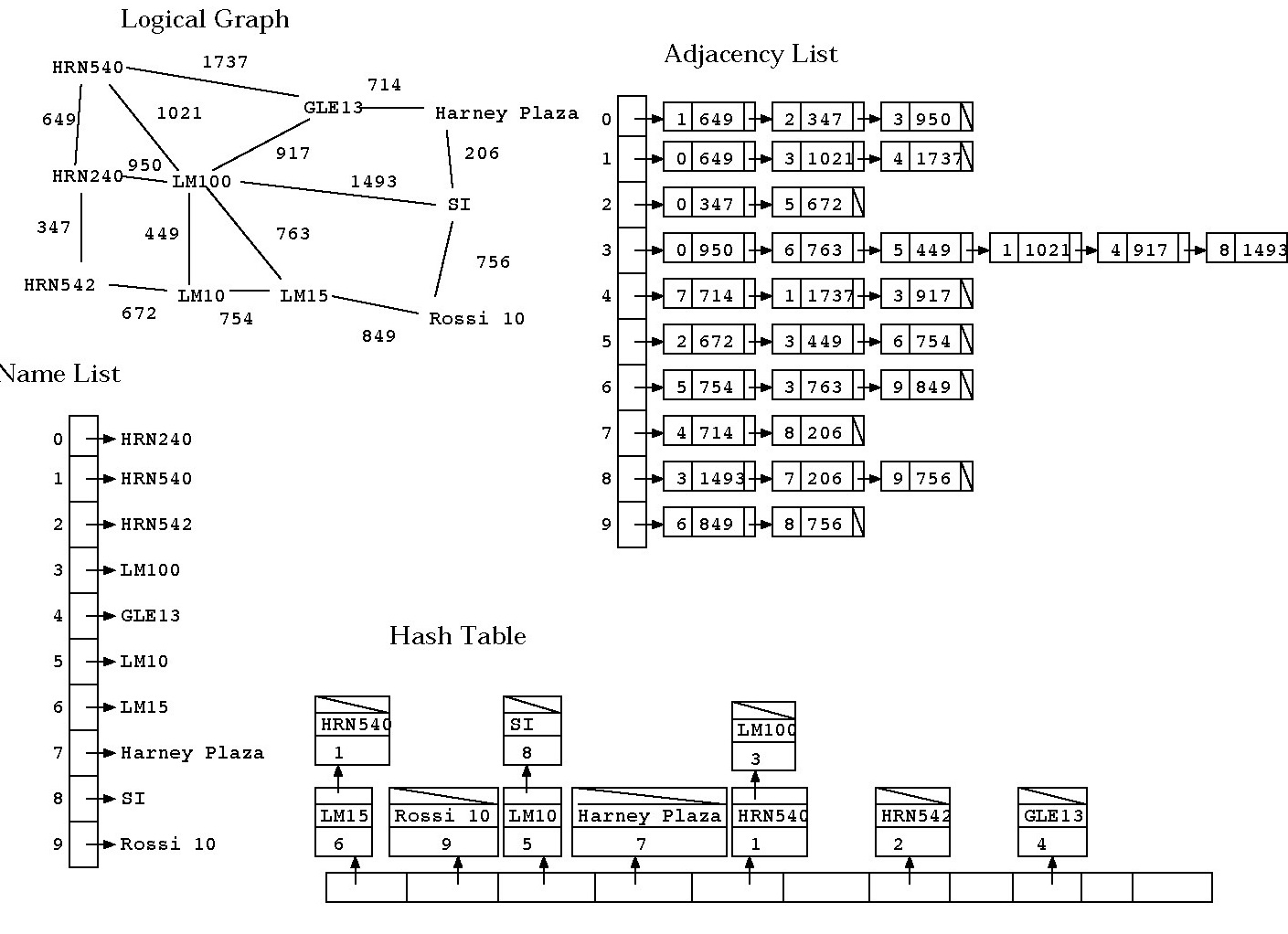
Data Structures

Input File Format:

The data file will have the following format:
The graphs for this project are undirected, so if there is an edge between vertices ``A'' and ``B'' in the graph with a cost of 4, then either Thus, the graph:
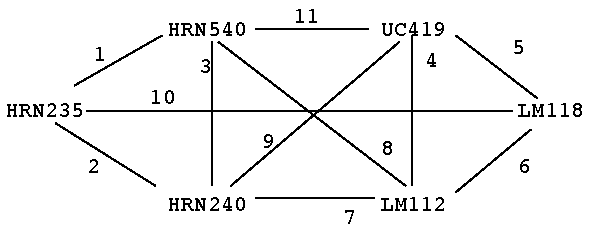
Sample Graph

could be represented by the input file:
HRN235
HRN540
HRN240
UC419
LM112
LM118
.
HRN235
HRN540
1
HRN540
HRN240
3
HRN240
HRN234
2
LM118
HRN245
10
HRN240
UC419
9
HRN240
LM112
7
HRN540
LM112
8
LM112
UC419
4
LM118
LM112
6
UC419
LM118
5
HRN540
UC419
11


Note that there is more than one way to represent this graph, since each edge can be represented in one of two ways, (V1, V2) or (V2, V1), and the edges and vertices can be listed in any order.

Program Output:


Your program should read in the graph from an input file specified by a command line argument and then: Thus, a legal output for the input file above would be:
Original Graph
HRN235 HRN540 1, HRN240 2, LM118, 10
HRN540 HRN235 1, HRN240 3, LM112 8, UC419 11
HRN240 HRN235 2, HRN540 3, UC419 9, LM112 7
UC419 HRN540 11, HRN240 9, LM112 4, LM118 5
LM112 HRN240 7, HRN540 8, UC419 4, LM118 6
LM118 UC419 5, HRN235 10, LM112 6
---------------------------------
Kruskal
HRN235 HRN540 1, HRN240 2 
HRN540 HRN235 1, 
HRN240 HRN235 2, LM112 7
UC419 LM112 4, LM118 5
LM112 HRN240 7, UC419 4
LM118 UC419 5
There is more than one legal output, since the adjacency lists can be in any order. This particular example has only one valid MST -- if a graph has multiple valid MSTs, you only need to find one of them. Note that you need two entries in the adjacency list for each edge in an undirected graph.

Project Submission

Submit all files required to run your project to:

https://www.cs.usfca.edu/svn/<username>/cs245/Bonus/

You can have any class names you like, as long as the main function is in a class named SpanningTree.

Random Details