Game Engineering Problems 1

CS 420 Game Engineering
Practice Problems #1

Assume the following for all problems:

Use row vectors (except question 10!)
Use a right-handed coordiate system.
All models point down the z axis in their object space (with "up" poining along y axis in object space)

Spaceship 1 has the rotation matrix (in world space):

m₁₁	m₁₂	m₁₃
m₂₁	m₂₂	m₂₃
m₃₁	m₃₂	m₃₃

And the position (in world space) [p_x, p_y, p_z]

You want to place Spaceship 2 directly in front of Spaceship 1 (in Spaceship 1's reference frame), 20 units away, pointing towards Spaceship 1. Spaceship 1 and spaceship 2 should have the same up vector.

Give the rotation matrix (in world space) and the position (in world space) of Spaceship 2

A character in your game has the rotation matrix (in world space)

m₁₁	m₁₂	m₁₃
m₂₁	m₂₂	m₂₃
m₃₁	m₃₂	m₃₃

And the position (in world space) [p_x, p_y, p_z]

You wish to place a camera 10 units directly to the right of the character, pointing at the character (that is, looking at the character's right shoulder), with the same up vector as the character.

Give the rotation matrix (in world space) and the position (in world space) of the camera.

A character in your game has the rotation matrix (in world space)

m₁₁	m₁₂	m₁₃
m₂₁	m₂₂	m₂₃
m₃₁	m₃₂	m₃₃

And the position (in world space) [p_x, p_y, p_z]

The ground is perpendicular to the world up vector. You wish to place a camera 10 units away from the character, along the line you get when you project the x axis to the ground plane. The camera should have the same up vector as as the world, and be pointed at the character. (See diagram) You can assume that [m_11, m_12,m₁₃] != [0, 1, 0] and [m_11, m_12,m₁₃] != [0, -1, 0] (so that x has a non-zero projection to the ground plane).

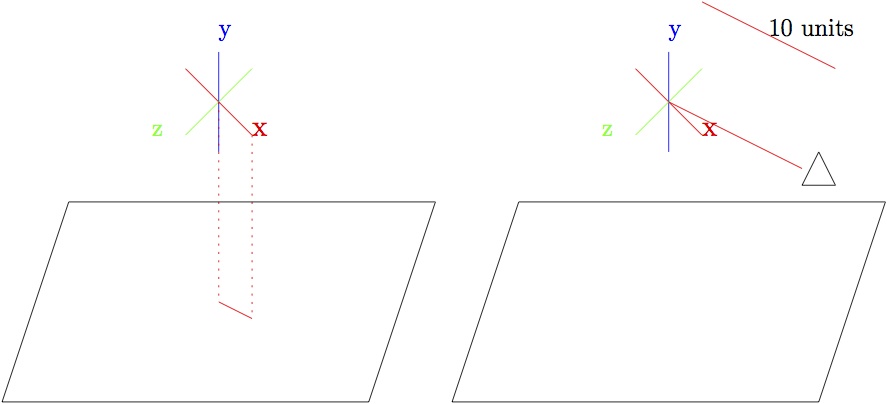
An object initially has the transformation vector

m₁₁	m₁₂	m₁₃
m₂₁	m₂₂	m₂₃
m₃₁	m₃₂	m₃₃

after applying a transform M, we are left with:

-m₁₁	-m₁₂	-m₁₃
-m₃₁	-m₃₂	-m₃₃
m₂₁	m₂₂	m₂₃

Does the transformation M contain a reflection?

Recall that quaternions are used to represent displacements (though they can also be used to represent absolute orientation, as a displacement from a reference orientation). For each of the following pairs of quaternions, describe how the displacement for quaternion 1 differes from the displacement for quaternion 2
1. [w, (x, y, z)] and [-w, (x, y, z)]
2. [w, (x, y, z)] and [w, (-x, -y, -z)]
3. [w, (x, y, z)] and [-w, (-x, -y, -z)]
4. [w, (x, y, z)] and [w, (-x, y, z)]
5. [w, (x, y, z)] and [w, (x, -y, z)]
6. [w, (x, y, z)] and [w, (x, y, -z)]
7. [w, (x, y, z)] and [w, (-x, -y, z)]
Describe the change in orientation described by the following quaternions:
1. [1, (0, 0, 0)]
2. [0, (0, 1, 0)]
3. [1/sqrt(2), (1/2, 1/2, 0)]
You have a spaceship whose position and orientation ore defined by the Ogre variables:
```
Ogre::Vector3 shipPos;
Ogre::Quaternion shipOrientation;
```
The spaceship has an orbiting satelite whose position and orientation (relative to the spaceship) are:
```
Ogre::Vector3 satelitePosLocal;
Ogre::Quaternion sateliteOrientationLocal;
```
1. Give code to calculate the position and orientation of the satelite in world space:
```
Ogre::Vector3 satelitePosGlobal = ...
Ogre::Quaternion sateliteOrientationGlobal = ...
```
2. You have a point in satelite space:
```
Ogre::Vector3 pointInSateliteSpace;
```
  Give code to transform that point into world space:
```
Ogre::Vector3 pointInWorldSpace = ...
```
3. You have a point in world space:
```
Ogre::Vector3 pointInWorldSpace;
```
  Give code to transform that point into satelite space:
```
Ogre::Vector3 pointInSateliteSpace = ...
```

Given the following bit of code:


class foo
{
    foo(int a, char *b, char *c) : x(a) {
       strcpy(y,b);
       z = new char[strlen(c) + 1];
       strcpy(z,c);
    }
    int x;
    char y[10];
    char *z;
};
class bar
{
   bar(int g, char * h, char *i) : d(g, h, i)
   {
      e = new foo(g, h, i);
   }
   foo d;
   foo *e;
};


int main()
{
   bar v(3, "hello", "there");
   bar *vPtr = new bar(5, "test", "string");
  // Point A
}

Show the contents of the stack and heap at Point A

Give the output of the following bit of code (WARNING: This is tricky. Trickier than you might think ...):

#include 

class A
{
public:
  void P1() {printf("P1 in A\n");}
  virtual void P2() {printf("P2 in A\n");}
  virtual void P3() {printf("P3 in A\n");}

};

class B : public A
{
public:
  void P1() {printf("P1 in B\n");}
  void P2() {printf("P2 in B\n");}
};


class C : public B
{
public:
  void P1() {printf("P1 in C\n");}
  void P2() {printf("P2 in C\n");}
  void P3() {printf("P3 in C\n");}
};


int main()
{
  A aVar;
  B bVar;
  C cVar;
  A *aPtr = new C();
  B *bPtr = new C();
  
  aVar.P1();
  aVar.P2();
  aVar.P3();
  printf("--------\n");
  bVar.P1();
  bVar.P2();
  bVar.P3();
  cVar.P1();
  cVar.P2();
  cVar.P3();
  printf("--------\n");
  aPtr->P1();
  aPtr->P2();
  aPtr->P3();
  bPtr->P1();
  bPtr->P2();
  bPtr->P3();
  printf("--------\n");
  aVar = cVar;
  aVar.P1();
  aVar.P2();
  aVar.P3();
  printf("--------\n");
  bVar = cVar;
  aPtr = &(bVar);
  aPtr->P1();
  aPtr->P2();
  aPtr->P3();
}

You have calcuated a series of transformations for a transforming a vector v (assuming v is a row vector) to get the result:
```
r = vABC
```
However, you now realize that your system uses column vectors instead of row vectors! Give a formula for the equivalent column vector r' (in terms of the column vector v', and the transformation matrices A, B, and C),