Queues
Overview of Queues
A queue is a first-in first-out data structure (FIFO). Conceptually, the
queue data structure behaves like a line. New data is placed at the rear of
the queue and when data is removed it is taken from the front. A printer
maintains a list of jobs in a queue; the oldest job, the one that has been in
the queue the longest, is serviced first.
The operations supported by a queue are as follows:
- void enqueue(Object o) - place object o on the rear of the queue
- Object dequeue() - remove and return the object at the front of the
queue
- Object front() - return the object at the front of the queue without
removing it
- int size() - return the size of the queue
- boolean isEmpty() - return true if the queue contains no elements,
false otherwise
Queues are typically depicted as follows:
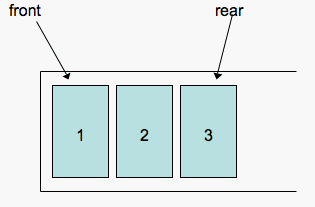
The previous queue would be the result of the following operations:
enqueue(1)
enqueue(2)
enqueue(3)
A dequeue on the queue above would return the object 1 and the resulting
queue would look as follows:
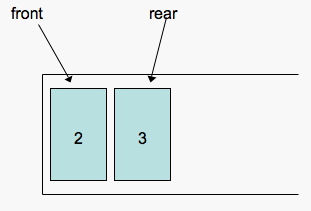
A front on the queue above would return the object 2 and the queue itself
would remain unchanged.
Implementation
A queue can be implemented using an array or a linked list. In essense,
the queue operations simply limit the way in which we access data stored in a
data structure such as an array. A queue can also be implemented using two
stacks and a stack using two queues. Though these implementations are not
terribly efficient, it is a good exercise to consider how you would build
such an implementation.
When choosing which rudimentary data structure to use for an
implementation, it is imperative that you consider efficiency. How many steps
will enqueue and dequeue require?
To implement a queue, you will need to implement a Queue class that
provides the queue operations described above. You will also want to provide
appropriate error reporting. Therefore, it might make sense to have the
dequeue operation throw a QueueEmptyException in the event that the
programmer tries to dequeue from a queue with no elements.
+Implementing a Queue Using an
Array
To implement a queue using an array, your Queue class will require an
array data member. The enqueue method will place a new object in the
appropriate location in the array. The dequeue method will return the
appropriate object from the array.
A queue with no elements will contain an array data member with no
elements. When the first element is enqueued, where should the element be
placed? You can place the element anywhere in the array, but position 0 makes
sense. The second element should be placed at position 1, and so on. After
enqueuing elements 1, 2, and 3, the conceptual model and underlying
implementation would look as follows:
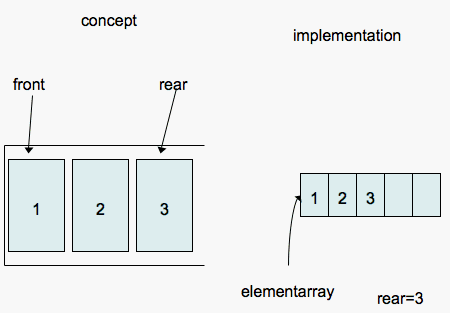
The pseudocode for enqueue would look as follows:
enqueue(o):
if rear -- elementarray.length
throw new QueueFullException
elementarray[rear++] = o
The big-oh running time of enqueue is constant.
Now, consider how you would implement dequeue. One option would be to
remove the 0th element (in this case 1) by moving all of the other elements
to the left. This, however, would be a costly O(N) operation. Fortunatley,
the operation can be implemented in O(1) time by using a circular
array.
To implement a circular array, you must maintain the index of the rear of
the queue and the index of the front of the queue. The general
algorithm for dequeue is as follows, though we'll next identify a problem
with this algorithm:
dequeue-first-cut():
if size > 0
tmp = elementarray[front]
front++
return tmp
else
throw new QueueEmptyException
The result of executing a deque on an array of three elements would look as
follows:
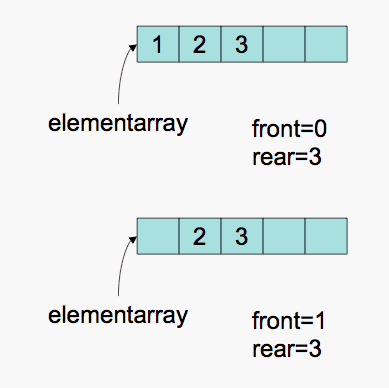
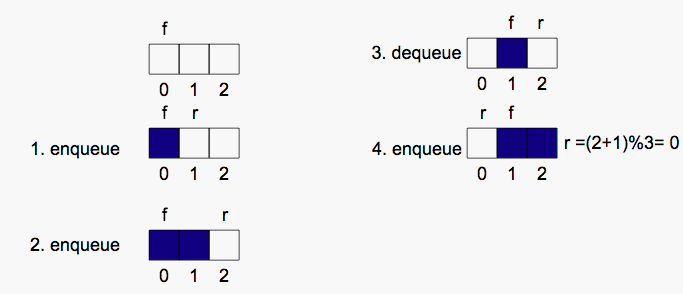
Next, consider what would happen if you were to enqueue N elements, where
N is the size of your element array, and then dequeue all N elements. Your
element array would be empty, seemingly indicating that you could enqueue
another element. However, using the preceeding algorithm, front would be N
and you would end up with an ArrayIndexOutOfBoundsException if you were to
attempt to place an element there. To take advantage of every empty slot in
your array, front and rear should wrap around to position 0 when the end of
the array is reached. This can be accomplished using modulo arithmetic.
Rather than simply incrementing front and rear as we have in the preceeding
algorithms, we set front = (front+1)%N and rear = (rear+1)%N. Following is a
complete example:
+Implementing a Queue Using a
Linked List
Implementing a queue using a linked list is much simpler than using an
array. Recall from the stacks lecture that as long
as we avoid using the removeTail operation we can achieve O(1) running time
for enqueue and dequeue. This can be easily accomplished by maintaining a
tail pointer and using insertTail to implement enqueue. Dequeue can then be
implemented by invoking removeHead.
Sami Rollins
Date: 2007-11-05


