We start by addressing the question of why process need to coordinate their actions and agree on values in various scenarios.
Coordination in a synchronous system with no failures is comparatively easy. We'll look at some algorithms targeted toward this environment. However, if a system is asynchronous, meaning that messages may be delayed an indefinite amount of time, or failures may occur, then coordination and agreement become much more challenging.
A correct process "is one that exhibits no failures at any point in the execution under consideration." If a process fails, it can fail in one of two ways: a crash failure or a byzantine failure. A crash failure implies that a node stops working and does not respond to any messages. A byzantine failure implies that a node exhibits arbitrary behavior. For example, it may continue to function but send incorrect values.
Failure Detection
One possible algorithm for detecting failures is as follows:
This seems ok if there are no failures. What happens if a failure occurs? In this case, q will not send a message. In a synchronous system, p waits for d seconds (where d is the maximum delay in message delivery) and if it does not hear from q then it knows that q has failed. In an asynchronous system, q can be suspected of failure after a timeout, but there is no guarantee that a failure has occurred.
The first set of coordination algorithms we'll consider deal with mutual exclusion. How can we ensure that two (or more) processes do not access a shared resource simultaneously? This problem comes up in the OS domain and is addressed by negotiating with shared objects (locks). In a distributed system, nodes must negotiate via message passing.
Each of the following algorithms attempt to ensure the following:
- Safety: At most one process may execute in the critical section (CS) at a time.
- Liveness: Requests to enter and exit the critical section eventually succeed.
- Causal ordering: If one request to enter the CS happened-before another, then entry to the CS is granted in that order.
Central Server
The first algorithm uses a central server to manage access to the shared resource. To enter a critical section, a process sends a request to the server. The server behaves as follows:
Requests are serviced in FIFO order.
If no failures occur, this algorithm ensures safety and liveness. However, ordering is not preserved (why?). The central server is also a bottleneck and a single point of failure.
Token Ring
The token ring algorithm arranges processes in a logical ring. A token is passed clockwise around the ring. When a process receives the token it can enter its critical section. If it does not need to enter a critical section, it immediately passes the token to the next process.
This algorithm also achieves safety and liveness, but not ordering, in the case when no failures occur. However, a significant amount of bandwidth is used because the token is passed continuously even when no process needs to enter a CS.
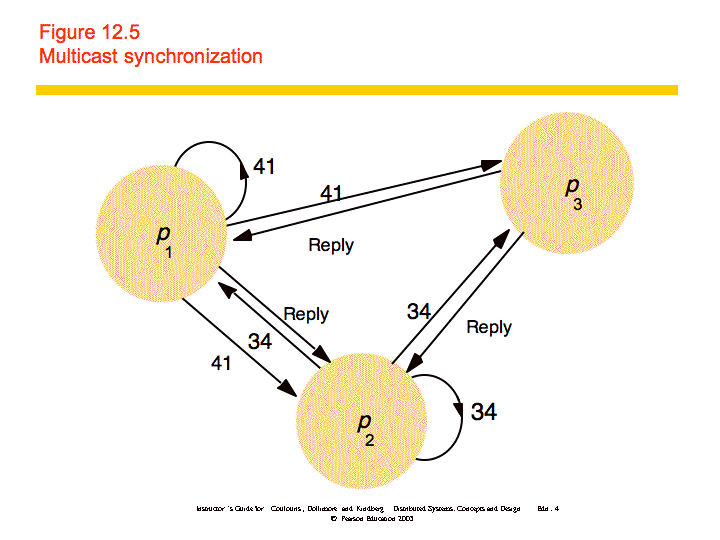
Multicast and Logical Clocks
Each process has a unique identifier and maintains a logical clock. A process can be in one of three states: released, waiting, or held. When a process wants to enter a CS it does the following:
When a message is received from another process, it does the following:
When a process exits a CS, it does the following:

This algorithm provides safety, liveness, and ordering. However, it cannot deal with failure and has problems of scale.
None of the algorithms discussed are appropriate for a system in which failures may occur. In order to handle this situation, we would need to first detect that a failure has occurred and then reorganize the processes (e.g., form a new token ring) and reinitialize appropriate state (e.g., create a new token).
An election algorithm determines which process will play the role of coordinator or server. All processes need to agree on the selected process. Any process can start an election, for example if it notices that the previous coordinator has failed. The requirements of an election algorithm are as follows:
Ring-based
Processes are arranged in a logical ring. A process starts an election by placing its ID and value in a message and sending the message to its neighbor. When a message is received, a process does the following:
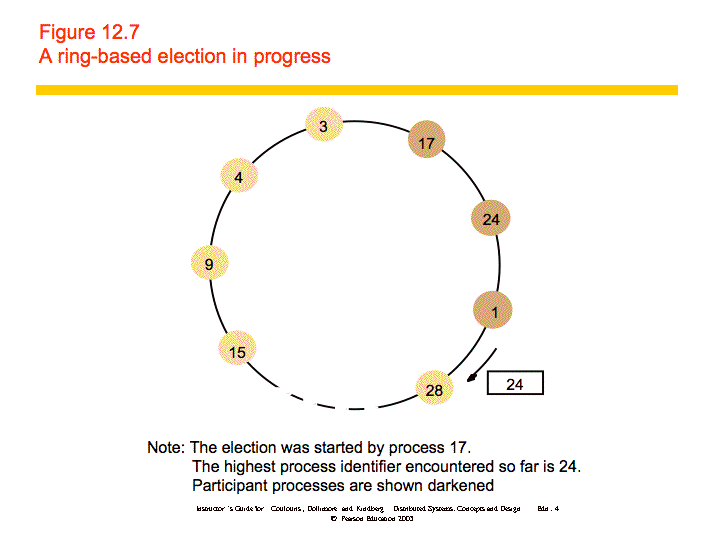
Safety is guaranteed - only one value can be largest and make it all the way through the ring. Liveness is guaranteed if there are no failures. However, the algorithm does not work if there are failures.
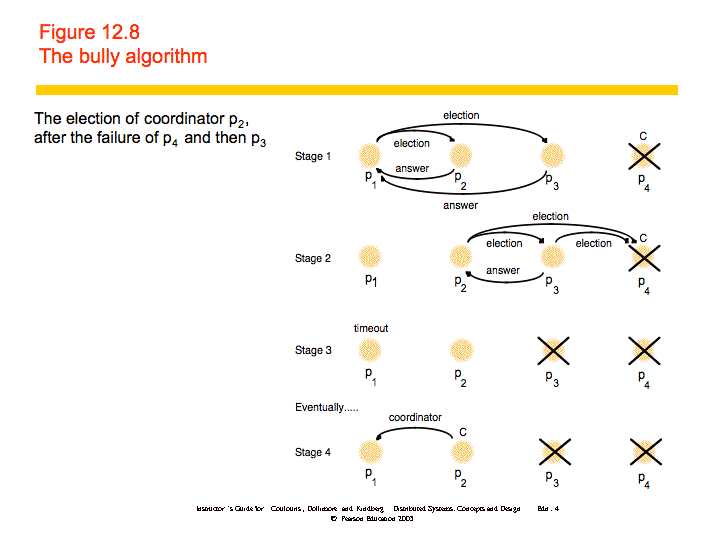
Bully
The bully algorithm can deal with crash failures, but not communication failures. When a process notices that the coordinator has failed, it sends an election message to all higher-numbered processes. If no one replies, it declares itself the coordinator and sends a new coordinator message to all processes. If someone replies, it does nothing else. When a process receives an election message from a lower-numbered process it returns a reply and starts an election. This algorithm guarantees safety and liveness and can deal with crash failures.
All of the previous algorithms are examples of the consensus problem: how can we get all processes to agree on a state? Here, we look at when the consensus problem is solvable.
The system model considers a collection of processes pi (i = 1, 2, ..., N). Communication is reliable, but processes may fail. Failures may be crash failures or byzantine failures.
The goals of consensus are as follows:
We consider the Byzantine Generals problem. A set of generals must agree on whether to attack or retreat. Commanders can be treacherous (faulty). This is similar to consensus, but differs in that a single process proposes a value that the others must agree on. The requirements are:
If communication is unreliable, consensus is impossible. Remember the blue army discussion from the second lecture period. With reliable communication, we can solve consensus in a synchronous system with crash failures.
We can solve Byzantine Generals in a synchronous system as long as less than 1/3 of the processes fail. The commander sends the command to all of the generals and each general sends the command to all other generals. If each correct process chooses the majority of all commands, the requirements are met. Note that the requirements do not specify that the processes must detect that the commander is fault.
It is impossible to guarantee consensus in an asynchronous system, even in the presence of 1 crash failure. That means that we can design systems that reach consensus most of the time, but cannot guarantee that they will reach consensus every time. Techniques for reaching consensus in an asynchronous system include the following: