There are two formal models of distributed systems: synchronous and asynchronous.
Synchronous distributed systems have the following characteristics:
- the time to execute each step of a process has known lower and upper bounds;
- each message transmitted over a channel is received within a known bounded time;
- each process has a local clock whose drift rate from real time has a known bound.
Asynchronous distributed systems, in contrast, guarantee no bounds on process execution speeds, message transmission delays, or clock drift rates. Most distributed systems we discuss, including the Internet, are asynchronous systems.
Generally, timing is a challenging an important issue in building distributed systems. Consider a couple of examples:
In the first example, we would really like to synchronize the clocks of all participating computers and take a measurement of absolute time. In the second and third examples, knowing the absolute time is not as crucial as knowing the order in which events occurred.
Every computer has a physical clock that counts oscillations of a crystal. This hardware clock is used by the computer's software clock to track the current time. However, the hardware clock is subject to drift -- the clock's frequency varies and the time becomes inaccurate. As a result, any two clocks are likely to be slightly different at any given time. The difference between two clocks is called their skew.
There are several methods for synchronizing physical clocks. External synchronization means that all computers in the system are synchronized with an external source of time (e.g., a UTC signal). Internal synchronization means that all computers in the system are synchronized with one another, but the time is not necessarily accurate with respect to UTC.
In a synchronous system, synchronization is straightforward since upper and lower bounds on the transmission time for a message are known. One process sends a message to another process indicating its current time, t. The second process sets its clock to t + (max+min)/2 where max and min are the upper and lower bounds for the message transmission time respectively. This guarantees that the skew is at most (max-min)/2.
Cristian's method for synchronization in asynchronous systems is similar, but does not rely on a predetermined max and min transmission time. Instead, a process p1 requests the current time from another process p2 and measures the RTT (Tround) of the request/reply. Whenp1 receives the time t from p2 it sets its time to t + Tround/2.
The Berkeley algorithm, developed for collections of computers running Berkeley UNIX, is an internal synchronization mechanism that works by electing a master to coordinate the synchronization. The master polls the other computers (called slaves) for their times, computes an average, and tells each computer by how much it should adjust its clock.
The Network Time Protocol (NTP) is yet another method for synchronizing clocks that uses a hierarchical architecture where he top level of the hierarchy (stratum 1) are servers connected to a UTC time source.
Physical time cannot be perfectly synchronized. Logical time provides a mechanism to define the causal order in which events occur at different processes. The ordering is based on the following:
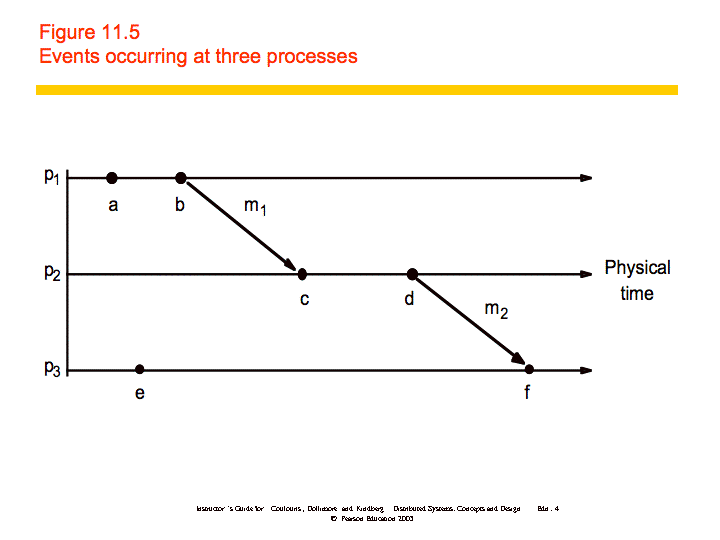
"Lamport called the partial ordering obtained by generalizing these two relationships the happened-before relation." ()

In the figure, and . Also, and , which means that . However, we cannot say that or vice versa; we say that they are concurrent
(a || e).
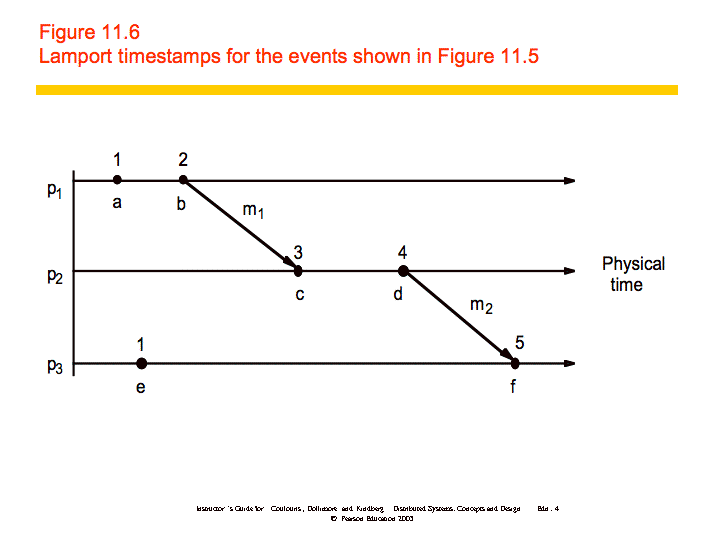
A Lamport logical clock is a monotonically increasing software counter, whose value need bear no particular relationship to any physical clock. Each process pi keeps its own logical clock, Li, which it uses to apply so-called Lamport timestamps to events.
Lamport clocks work as follows:
- LC1: Li is incremented before each event is issued at pi.
- LC2:
- When a process pi sends a message m, it piggybacks on m the value t = Li.
- On receiving (m, t), a process pj computes Lj := max(Lj, t) and then applies LC1 before timestamping the event receive(m).
An example is shown below:
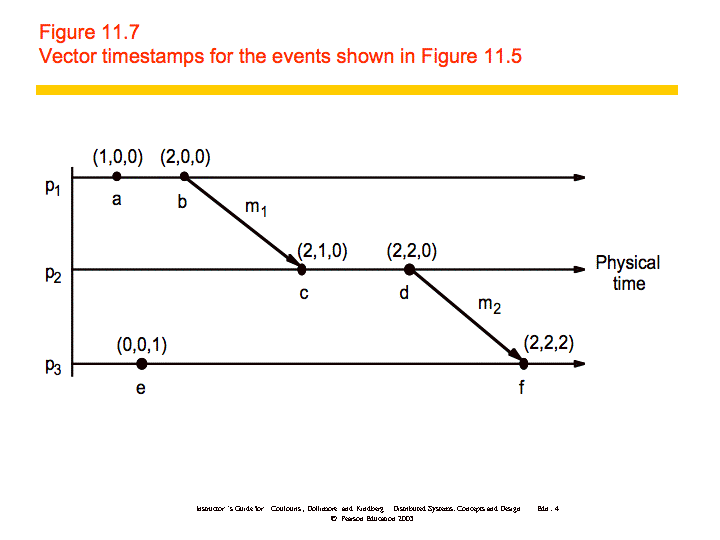
If then L(e) < L(e'), but the converse is not true. Vector clocks address this problem. "A vector clock for a system of N processes is an array of N integers." Vector clocks are updated as follows:
VC1: Initially, Vi[j] = 0 for i, j = 1, 2, ..., N
VC2: Just before pi timestamps an event, it sets Vi[i]:=Vi[i]+1.
VC3: pi includes the value t = Vi in every message it sends.
VC4: When pi receives a timestamp t in a message, it sets Vi[j]:=max(Vi[j], t[j]), for 1, 2, ...N. Taking the componentwise maximum of two vector timestamps in this way is known as a merge operation.
An example is shown below:
Vector timestamps are compared as follows:
V=V' iff V[j] = V'[j] for j = 1, 2, ..., N
V <= V' iff V[j] <=V'[j] for j = 1, 2, ..., N
V < V' iff V <= V' and V !=V'
If then V(e) < V(e') and if V(e) < V(e') then .
It is often desirable to determine whether a particular property is true of a distributed system as it executes. We'd like to use logical time to construct a global view of the system state and determine whether a particular property is true. A few examples are as follows:
In general, this problem is referred to as Global Predicate Evaluation. "A global state predicate is a function that maps from the set of global state of processes in the system ρ to {True, False}."
Because physical time cannot be perfectly synchronized in a distributed system it is not possible to gather the global state of the system at a particular time. Cuts provide the ability to "assemble a meaningful global state from local states recorded at different times".
Definitions:
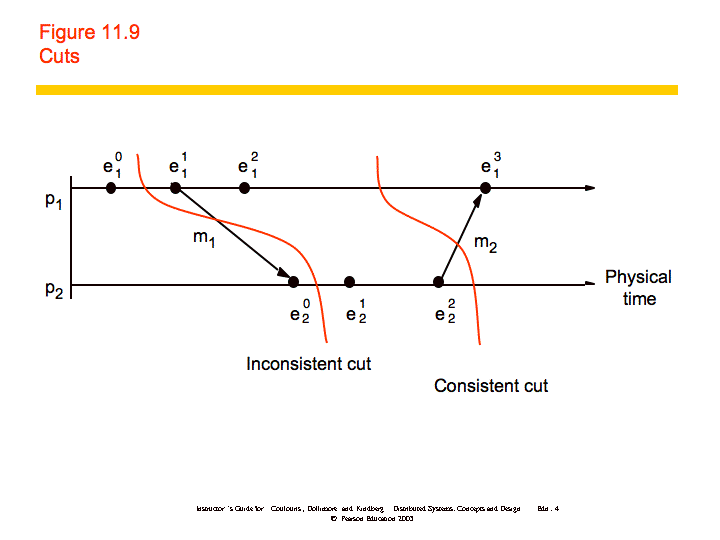
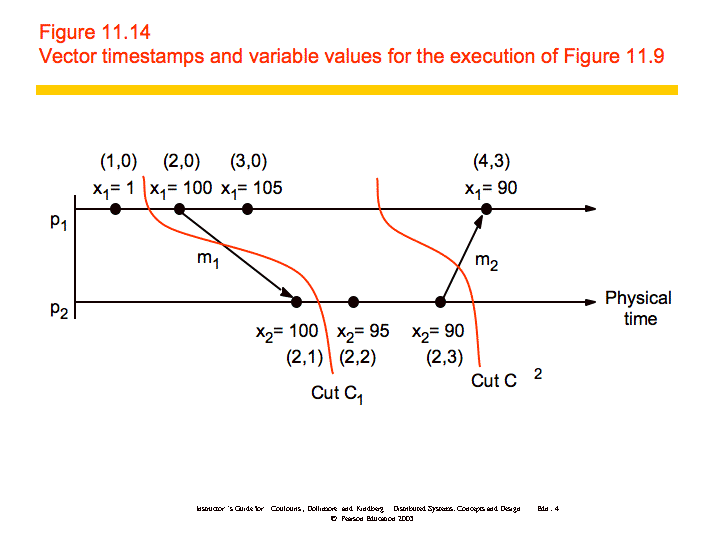
To further examine how you might produce consistent cuts, we'll use the distributed debugging example. Recall that we have several processes, each with a variable xi. "The safety condition required in this example is |xi-xj| <= δ (i, j = 1, 2, ..., N)."
The algorithm we'll discuss is a centralized algorithm that determines post hoc whether the safety condition was ever violated. The processes in the system, p1, p2, ..., pN, send their states to a passive monitoring process, p0. p0 is not part of the system. Based on the states collected, p0 can evaluate the safety condition.
Collecting the state: The processes send their initial state to a monitoring process and send updates whenever relevant state changes, in this case the variable xi. In addition, the processes need only send the value of xi and a vector timestamp. The monitoring process maintains a an ordered queue (by the vector timestamps) for each process where it stores the state messages. It can then create consistent global states which it uses to evaluate the safety condition.
Let S = (s1, s2, ..., SN) be a global state drawn from the state messages that the monitor process has received. Let V(si) be the vector timestamp of the state si received from pi. Then it can be shown that S is a consistent global state if and only if:
V(si)[i] >= V(sj)[i] for i, j = 1, 2, ..., N