Time Synchronization

Overview

Generally, timing is a challenging an important issue in building distributed systems. Consider a couple of examples:

• A distributed, real time auction where the system must know which of two bidders submitted their bid first.
• A TDMA protocol that requires coordination among sensor nodes.
• A MAC protocol that requires coordination among sensor nodes.
• An application that determines the angle of arrival of an acoustic signal by analyzing the times at which the signal reaches an array of sensors.

Clock Synchronization

Every computer has a physical clock that counts oscillations of a crystal. This hardware clock is used by the computer's software clock to track the current time. However, the hardware clock is subject to drift -- the clock's frequency varies and the time becomes inaccurate. As a result, any two clocks are likely to be slightly different at any given time. Ganeriwal reports that motes can lose up to 40 microseconds every second.  The difference between two clocks is called their skew.

There are several methods for synchronizing physical clocks. External synchronization means that all computers in the system are synchronized with an external source of time (e.g., a UTC signal). Internal synchronization means that all computers in the system are synchronized with one another, but the time is not necessarily accurate with respect to UTC.  

In a system that provides guaranteed bounds on message transmission time, synchronization is straightforward since upper and lower bounds on the transmission time for a message are known. One process sends a message to another process indicating its current time, t. The second process sets its clock to t + (max+min)/2 where max and min are the upper and lower bounds for the message transmission time respectively. This guarantees that the skew is at most (max-min)/2.

Cristian's method for synchronization in systems that do not provide such guarantees is similar, but does not rely on a predetermined max and min transmission time. Instead, a process p₁ requests the current time from another process p₂ and measures the RTT (T_round) of the request/reply. Whenp₁ receives the time t from p₂ it sets its time to t + T_round/2.

The Berkeley algorithm, developed for collections of computers running Berkeley UNIX, is an internal synchronization mechanism that works by electing a master to coordinate the synchronization. The master polls the other computers (called slaves) for their times, computes an average, and tells each computer by how much it should adjust its clock.

The Network Time Protocol (NTP) is yet another method for synchronizing clocks that uses a hierarchical architecture where he top level of the hierarchy (stratum 1) are servers connected to a UTC time source such as a GPS unit.  The TPSN protocol is very similar to NTP.

Synchronization in WSN

• Physical time versus logical time
• External versus internal synchronization
• A priori versus posteriori synchronization - post-facto synchronization in WSN has been proposed in several papers.  Post-facto synchronization happens on demand, after the event occurs.  In this way, synchronization -- which requires resources such as energy -- only happens when necessary.  

• Precision - synchronization error
• Energy cost 
• Memory requirements
• Fault tolerance
• Scalability

• Send time - Time for the packet to pass from the application layer to the MAC layer -- highly variable based on delays introduced by OS.
• Access time - Time the MAC layer must wait for the channel to become free -- highly variable based on make protocol and one of the most critical factors contributing to delay.
• Transmission time - Time to transmit entire packet -- mainly deterministic and can be estimated based on packet size and radio speed.
• Propagation time - Time to traverse the link -- typically negligible in WSN.
• Reception time - Time for the receiver radio to receive bits and pass to MAC layer -- mainly deterministic.
• Receive time - Time  for MAC layer to construct packet and send to application layer -- changes based on delays of OS.

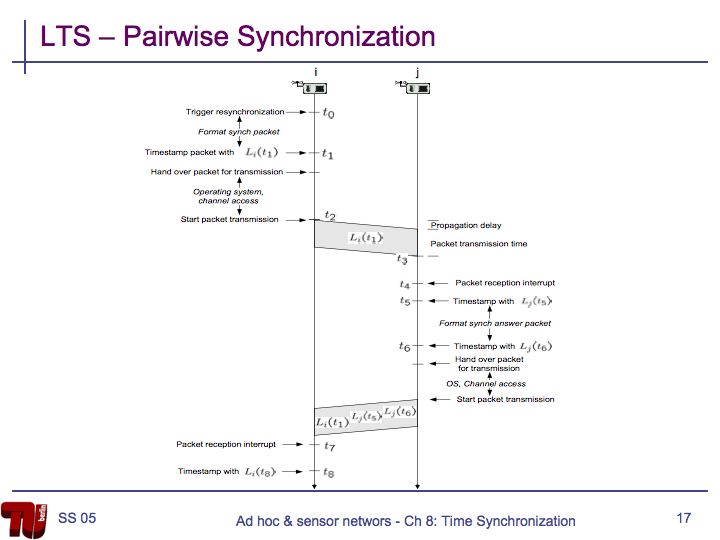
TPSN Overview

1. Level Discovery - Create a hierarchical topology in the network, similar to NTP.  The root node at level 0 may be synchronized with UTC time, for example using a GPS receiver.
2. Synchronization Phase - nodes at level i synchronize to a node at level i-1.

Level Discovery

• Root broadcasts a level_discovery packet containing the level and identity of the sender.
• Receivers assign themselves a level one greater than the level of the sender.
• Receivers broadcast a new level_discovery packet containing their level.
• Once a node is assigned a level it ignores future level_discovery packets.

Synchronization Phase

• Use sender-receiver synchronization to synchronize nodes at level i with nodes at level i-1.
• At time T1 node A sends a synchronization_pulse to node B.  The packet contains A's level and the value T1.
• Node B receives the packet at time T2 and sends an ACK at time T3.  This packet contains the values T1, T2, and T3.
• Node A receives the ACK at time T4.
• Assuming that clock drift and propagation delay do not change between T1 and T4, the clock drift can be calculated as:
• ((T2-T1) - (T4-T3))/2
• The propagation delay can be calculated as:
• ((T2-T1) + (T4-T3))/2
• The root initiates synchronization by broadcasting a time_sync packet.
• Receivers at level 1 wait for a random amount of time (to avoid collision) and send the synchronization_pulse to the root.
• Nodes at level 2 will hear the synchronization_pulse of nodes at level 1, backoff for a random time, and send a synchronization_pulse.

Special Provisions

• Nodes can proactively join the network by sending a level_request message.  Neighbors respond and the requesting node can assign itself a level.
• If a node's parent dies, the node will eventually timeout and send a level_request to rejoin the network.
• If the root dies, the remaining nodes can execute a leader election algorithm and the elected leader will take over the responsibilities of the root.

Reference-Broadcast Synchronization (RBS)

• A sender broadcasts a reference packet.
• Receivers i and j in the same broadcast domain receive the broadcast and record their local times.
• Receivers i and j exchange their observations to determine the offset of their clocks.

Logical Time

Physical time cannot be perfectly synchronized. Logical time provides a mechanism to define the causal order in which events occur at different processes. The ordering is based on the following:

• Two events occurring at the same process happen in the order in which they are observed by the process.
• If a message is sent from one process to another, the sending of the message happened before the receiving of the message.
• If e occurred before e' and e' occurred before e" then e occurred before e".

"Lamport called the partial ordering obtained by generalizing these two relationships the happened-before relation." ($\to$)

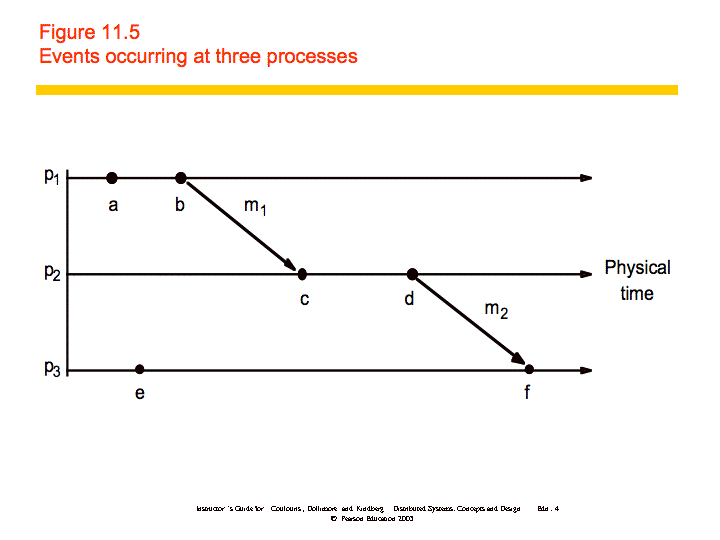
In the figure, $a\to b$ and $c\to d$. Also, $b\to c$and $d\to f$, which means that $a\to f$. However, we cannot say that $a\to e$or vice versa; we say that they are concurrent

(a || e).

A Lamport logical clock is a monotonically increasing software counter, whose value need bear no particular relationship to any physical clock. Each process p_i keeps its own logical clock, L_i, which it uses to apply so-called Lamport timestamps to events.

Lamport clocks work as follows:

• LC1: L_i is incremented before each event is issued at p_i.
• LC2:
• • When a process p_i sends a message m, it piggybacks on m the value t = L_i.
  • On receiving (m, t), a process p_j computes L_j := max(L_j, t) and then applies LC1 before timestamping the event receive(m).

An example is shown below:

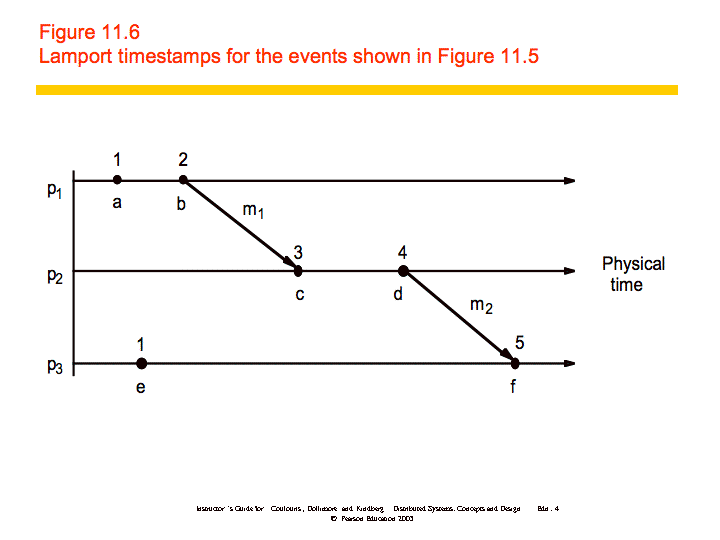
If $e\to e\text{'}$then L(e) < L(e'), but the converse is not true. Vector clocks address this problem. "A vector clock for a system of N processes is an array of N integers." Vector clocks are updated as follows:

VC1: Initially, V_i[j] = 0 for i, j = 1, 2, ..., N

VC2: Just before p_i timestamps an event, it sets V_i[i]:=V_i[i]+1.

VC3: p_i includes the value t = V_i in every message it sends.

VC4: When p_i receives a timestamp t in a message, it sets V_i[j]:=max(V_i[j], t[j]), for 1, 2, ...N. Taking the componentwise maximum of two vector timestamps in this way is known as a merge operation.

An example is shown below:

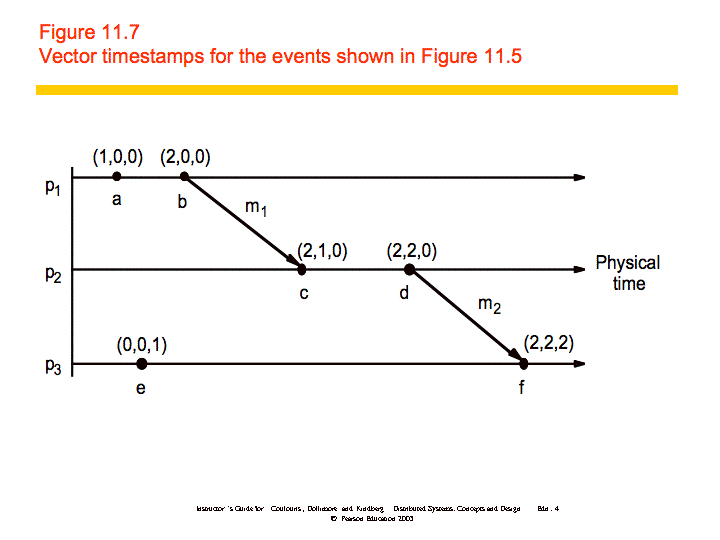
Vector timestamps are compared as follows:

V=V' iff V[j] = V'[j] for j = 1, 2, ..., N

V <= V' iff V[j] <=V'[j] for j = 1, 2, ..., N

V < V' iff V <= V' and V !=$$V'

If $e\to e\text{'}$then V(e) < V(e') and if V(e) < V(e') then $e\to e\text{'}$.

Global States

It is often desirable to determine whether a particular property is true of a distributed system as it executes. We'd like to use logical time to construct a global view of the system state and determine whether a particular property is true. A few examples are as follows:

• Distributed garbage collection: Are there references to an object anywhere in the system? References may exist at the local process, at another process, or in the communication channel.
• Distributed deadlock detection: Is there a cycle in the graph of the "waits for" relationship between processes?
• Distributed termination detection: Has a distributed algorithm terminated?
• Distributed debugging: Example: given two processes p₁ and p₂ with variables x₁ and x₂ respectively, can we determine whether the condition |x₁-x₂| > δ is ever true.

In general, this problem is referred to as Global Predicate Evaluation. "A global state predicate is a function that maps from the set of global state of processes in the system ρ to {True, False}."

• Safety - a predicate always evaluates to false. A given undesirable property (e.g., deadlock) never occurs.
• Liveness - a predicate eventually evaluates to true. A given desirable property (e.g., termination) eventually occurs.

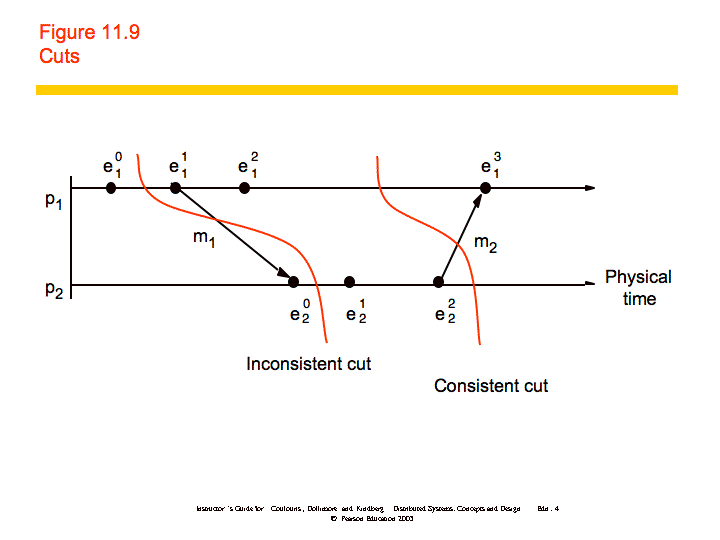
Cuts

Because physical time cannot be perfectly synchronized in a distributed system it is not possible to gather the global state of the system at a particular time. Cuts provide the ability to "assemble a meaningful global state from local states recorded at different times".

Definitions:

• ρ is a system of N processes p_i (i = 1, 2, ..., N)
• history(p_i) = h_i = <$e_i^0$, $e_i^1$,...>
• $h_i^k$=<$e_i^0$, $e_i^1$,..., $e_i^k$> - a finite prefix of the process's history
• $s_i^k$is the state of the process p_i immediately before the kth event occurs
• All processes record sending and receiving of messages. If a process p_i records the sending of message m to process p_j and p_j has not recorded receipt of the message, then m is part of the state of the channel between p_i and p_j.
• A global history of ρ is the union of the individual process histories: H = h₀ $\cup$h₁ ∪ h₂ ∪...∪h_N-1
• A global state can be formed by taking the set of states of the individual processes: S = (s₁, s₂, ..., s_N)
• A cut of the system's execution is a subset of its global history that is a union of prefixes of process histories (see figure below).
• The frontier of the cut is the last state in each process.
• A cut is consistent if, for all events e and e':
  • ($e\in C$ and $e\text{'}\to e$) $\Rightarrow e\text{'}\in C$
• A consistent global state is one that corresponds to a consistent cut.

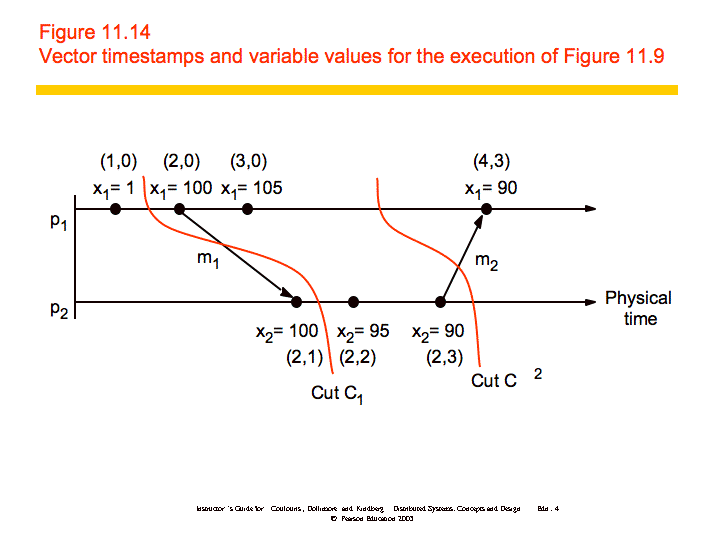
Distributed Debugging

To further examine how you might produce consistent cuts, we'll use the distributed debugging example. Recall that we have several processes, each with a variable x_i. "The safety condition required in this example is |x_i-x_j| <= δ (i, j = 1, 2, ..., N)."

The algorithm we'll discuss is a centralized algorithm that determines post hoc whether the safety condition was ever violated. The processes in the system, p₁, p₂, ..., p_N, send their states to a passive monitoring process, p₀. p₀ is not part of the system. Based on the states collected, p₀ can evaluate the safety condition.

Collecting the state: The processes send their initial state to a monitoring process and send updates whenever relevant state changes, in this case the variable x_i. In addition, the processes need only send the value of x_i and a vector timestamp. The monitoring process maintains a an ordered queue (by the vector timestamps) for each process where it stores the state messages. It can then create consistent global states which it uses to evaluate the safety condition.

Let S = (s₁, s₂, ..., S_N) be a global state drawn from the state messages that the monitor process has received. Let V(s_i) be the vector timestamp of the state s_i received from p_i. Then it can be shown that S is a consistent global state if and only if:

V(s_i)[i] >= V(s_j)[i] for i, j = 1, 2, ..., N

Date: 2008-01-15